May 7, 2019 Jill Gough

Multiplication Fact Fluency prototype – feedback requested

April 10, 2019April 10, 2019 Jill Gough

#TrinityLearns Leading Learners to Level Up as a TEAM (#LL2LU) Part 2

March 13, 2019April 10, 2019 Jill Gough

#TrinityLearns Leading Learners to Level Up as a TEAM (#LL2LU)

October 22, 2018 Jill Gough

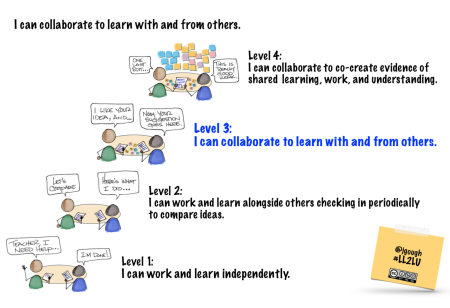
Collaboration – How might we level up again?

October 13, 2018October 15, 2018 Jill Gough

Collaboration – How might we level up?

September 12, 2018October 16, 2018 Jill Gough

Agenda: Embolden Your Inner Mathematician (09.12.18) Week 2

August 29, 2018August 30, 2018 Jill Gough

Establish goals to focus learning – Reading Workshop 5th Grade

March 29, 2018March 29, 2018 Jill Gough

I can elicit and use evidence of student thinking #NCTMP2A #LL2LU

March 27, 2018March 27, 2018 Jill Gough

I can establish mathematics goals to focus learning #NCTMP2A #LL2LU

January 10, 2018 Jill Gough

I’ll help you recover…