February 22, 2023February 21, 2023 Jill Gough

Listening for Learning: Are learners growing in the SMPs? (part 1)

April 10, 2019April 10, 2019 Jill Gough

#TrinityLearns Leading Learners to Level Up as a TEAM (#LL2LU) Part 2

March 13, 2019April 10, 2019 Jill Gough

#TrinityLearns Leading Learners to Level Up as a TEAM (#LL2LU)

November 7, 2018 Jill Gough

Agenda: Embolden Your Inner Mathematician (11.07.18) Week 8

October 24, 2018October 25, 2018 Jill Gough

Agenda: Embolden Your Inner Mathematician (10.24.18) Week 7

October 22, 2018 Jill Gough

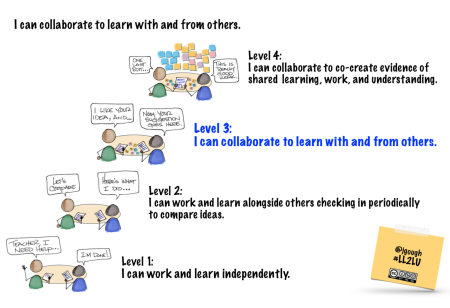
Collaboration – How might we level up again?

October 13, 2018October 15, 2018 Jill Gough

Collaboration – How might we level up?

October 10, 2018October 16, 2018 Jill Gough

Agenda: Embolden Your Inner Mathematician (10.10.18) Week 5

October 3, 2018October 16, 2018 Jill Gough

Agenda: Embolden Your Inner Mathematician (10.03.18) Week 4

September 26, 2018 Jill Gough

Focus on Learning: Establish Mathematics Goals to Focus Learning