February 5, 2020 Jill Gough

Learn, not memorize (within playing with sentences)

January 23, 2020January 23, 2020 Jill Gough

Mentor Sentence: Notice, Emulate, Learn #LL2LU

January 20, 2020January 20, 2020 Jill Gough

Fear of imperfection; deep practice; just make a mark

October 22, 2018 Jill Gough

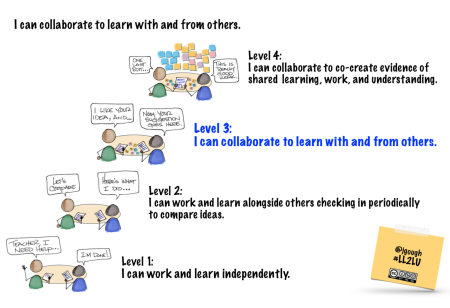
Collaboration – How might we level up again?

October 13, 2018October 15, 2018 Jill Gough

Collaboration – How might we level up?

September 26, 2018 Jill Gough

Focus on Learning: Establish Mathematics Goals to Focus Learning

August 29, 2018August 30, 2018 Jill Gough

Establish goals to focus learning – Reading Workshop 5th Grade

August 27, 2018August 27, 2018 Jill Gough

Using number lines to build strong, deep academic foundation

August 17, 2018August 26, 2018 Jill Gough

Lesson Study: different teachers, common lesson plan, guaranteed and viable curriculum

August 8, 2018August 26, 2018 Jill Gough

Focus on Instructional Core: establish goals to focus learning