Experiments in Learning by Doing

Seeking brightspots and dollups of feedback about learning and growth.

Menu Skip to content
  • Home
  • #LL2LU Learning Progressions: SMP
    • #LL2LU Learning Progressions
    • #LL2LU Learning Progressions #NCTMP2A
  • About Jill Gough
    • Awards
    • Presentations
    • Resume
  • Jill’s Reading List
    • Reading List for Mathematizing Read Alouds
  • Jill’s TED Talk List
  • PD Courses
  • Talks captured on video

Category: Ask Don’t Tell

October 22, 2018 Jill Gough

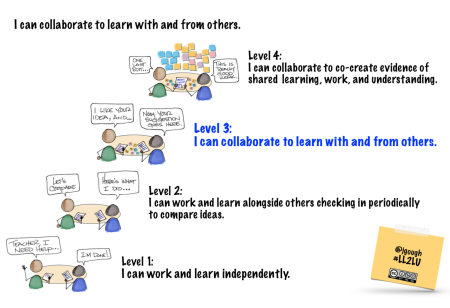
Collaboration – How might we level up again?

October 13, 2018October 15, 2018 Jill Gough

Collaboration – How might we level up?

October 18, 2017October 19, 2017 Jill Gough

Embolden Your Inner Mathematician: week 7 agenda

October 11, 2017October 18, 2017 Jill Gough

Embolden Your Inner Mathematician: week 6 agenda

October 4, 2017October 9, 2017 Jill Gough

Embolden Your Inner Mathematician: week 5 agenda

September 27, 2017September 27, 2017 Jill Gough

Embolden Your Inner Mathematician: week 4 agenda

September 20, 2017September 19, 2017 Jill Gough

Embolden Your Inner Mathematician: week 3 agenda

September 9, 2017September 8, 2017 Jill Gough

Embolden Your Inner Mathematician Week 1: Number Talks

June 7, 2017June 7, 2017 Jill Gough

Summer PD: Day 3 Empower Learners

April 12, 2017April 12, 2017 Jill Gough

Building and Sustaining the Culture of Problem Solving in our Classroom with @FawnPNguyen #MtHolyokeMath

Posts navigation

Older posts

Past posts:

#Sketchnotes to Learn: Jill Gough notes

The Writing Revolution: Advancing Thinking Through Writing K-2 Session 4 (day 2 session 2) @TheWritingRevol

The Writing Revolution: Advancing Thinking Through Writing K-2 Session 4 (day 2 session 2) @TheWritingRevol

The Writing Revolution: Advancing Thinking Through Writing K-2 Session 3 (day 2 session 1) @TheWritingRevol

The Writing Revolution: Advancing Thinking Through Writing K-2 Session 3 (day 2 session 1) @TheWritingRevol

The Writing Revolution: Advancing Thinking Through Writing K-2 Day 1 Session 2 @TheWritingRevol

The Writing Revolution: Advancing Thinking Through Writing K-2 Day 1 Session 2 @TheWritingRevol

Thinking about:

#LL2LU Algebra Ask Don't Tell Assessment Conferences Connecting Ideas Creativity Grading Information Age Learning Learning Learning Progressions Math-Science Connections PBL Peer Observations PLC Presentations Professional Development Feedback Professional Development Plans Questions Reading Reflection Sketch Notes Social-Emotional Social Media Summer Reading Synergy 8 Teachnology Technology TED talk Time

Enter your email address to subscribe to this blog and receive notifications of new posts by email.

Join 5,488 other subscribers

#LL2LU SMPs and more

smp-1_ll2lu_make_sense_persevere
smp-3_ll2lu_construct_argument
ShowYourWork-ES
smp-8_ll2lu_regularity_repeated_reasoning
ll2lu_Math_Flexibility
smp-7_ll2lu_make_use_structure

Noticing and noting

My Tweets

Goodreads

Follow Experiments in Learning by Doing on WordPress.com
Blog at WordPress.com.
Experiments in Learning by Doing
Blog at WordPress.com.
  • Follow Following
    • Experiments in Learning by Doing
      • Join 178 other followers
    • Already have a WordPress.com account? Log in now.
    • Experiments in Learning by Doing
    • Customize
    • Follow Following
    • Sign up
    • Log in
    • Report this content
    • View site in Reader
    • Manage subscriptions
    • Collapse this bar
 

Loading Comments...