At Trinity School, we believe that every child can become a successful mathematician.  Thinking critically, problem-solving, and demonstrating number flexibility lead students to make connections to the real world.  Our students learn that mistakes are a necessary part of growth and learning.  Taking the time to reflect, question, share, and listen to others deepens mathematical understanding. 

Through play and hands-on exploration, children learn how to make connections, organize information, and persevere in solving problems.  We are committed to instilling a lifelong love of mathematics by providing engaging and challenging opportunities to learn through making mistakes, productive struggle, and perseverance which leads to success.

Student learning goals include:

• Making sense of problems and persevering in solving them
• Building confidence and competence by taking risks and learning from successes and failures
• Developing flexibility, fluency, and efficiency of skills and processes
• Attending to precision with math vocabulary and symbols
• Building conceptual understanding, moving from the concrete to the abstract
• Developing and applying multiple strategies for solving problems
• Constructing mathematical arguments and kindly offering helpful feedback to others
• Transferring and applying mathematical concepts across the curriculum
• Deliberately reflecting throughout the learning process

Trinity has an internally developed series of PD courses for our faculty. These job-embedded courses focus on why, what, and how to build numeracy skills with our students. As part of our mission as a community of learners, and at their request, we also developed a series for parents.

The meeting’s interactive agenda for parents included tasks we use with our student to highlight and demonstrate why and how we teach our students to listen, speak, read, and write like mathematicians.

We want all of our students to learn to speak like a mathematician. Mathematicians use precise language to share what they notice.

So that we model what we do in our classrooms, we started with a task from wodb.ca, which addresses many of our student goals.

One of these things is not like the others; one of these things is just not the same. Take a minute to decide which one is not like the others and why.

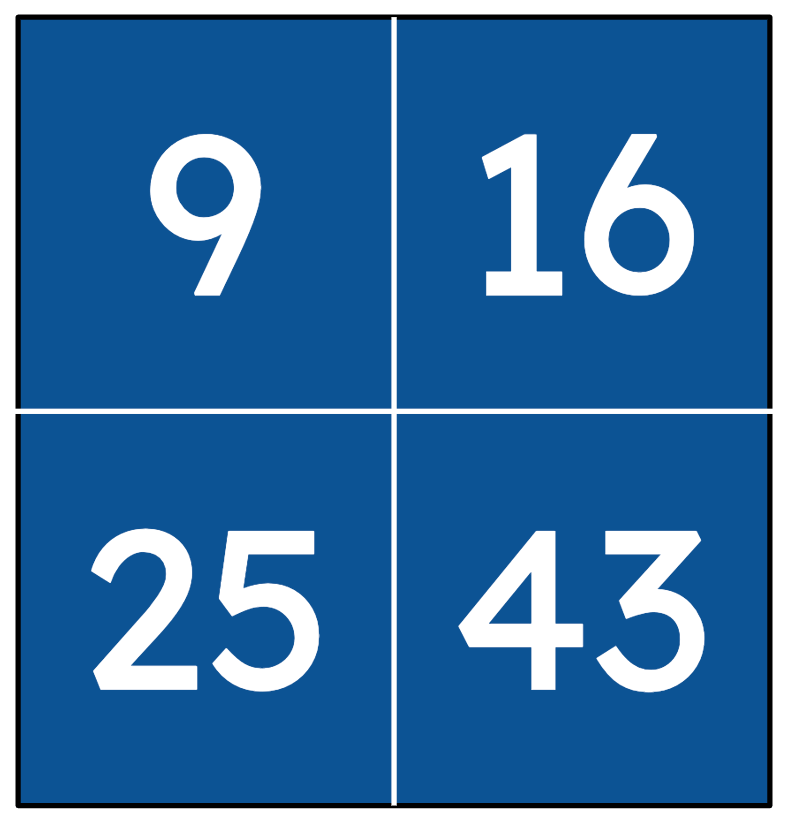
Parents were asked to make an argument that one of the four choices is different from the others. After a minute of quiet think time, we asked them to pick a partner and discuss their answer and rationale. Answers included “Nine is the only single-digit number.” “43 is the only prime number.” “43 is the only number that is not a perfect square.” “25 is the only multiple of 5.” “16 is the only even number and the only multiple of four.” “9 is the only multiple of three.“

Do you see how much vocabulary and precise language can be offered from this task?

• Making sense of problems and persevering in solving them
• Building confidence and competence by taking risks and learning from successes and failures
• Developing flexibility, fluency, and efficiency of skills and processes
• Attending to precision with math vocabulary and symbols

We want all of our students to learn to read like a mathematician. Mathematicians pay attention to quantities and relationships in a problem statement.

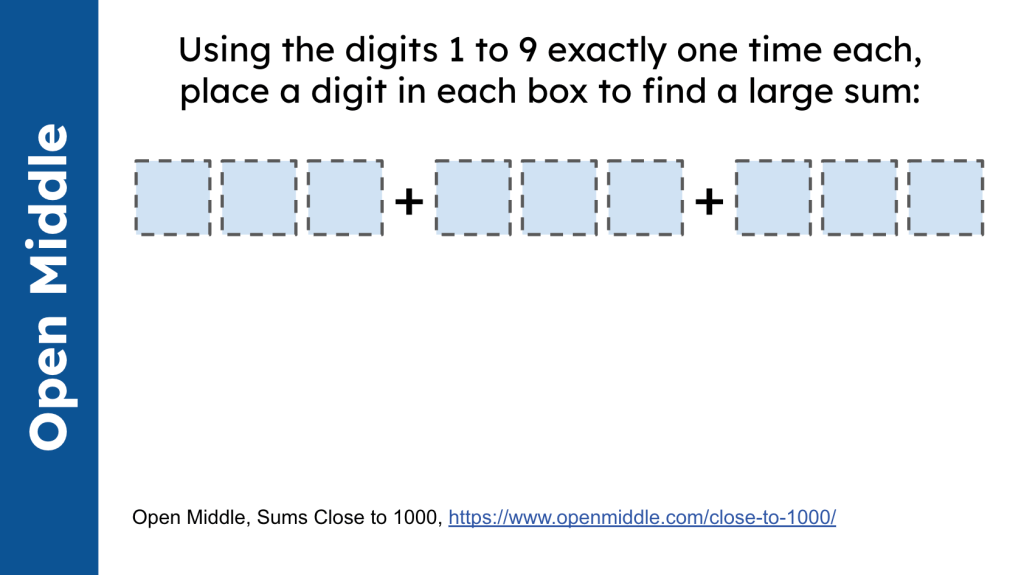
Robert Kaplinsky’s original Open Middle task, Sums Close to 1000, asks learners to place a digit in each box to make the sum as close to 1000 as possible, using the digits 1 to 9 exactly one time each. We explained to parents first we want students to experience success. Any sum will do. Then, we pair and share. Did you all have the same expression? What was the sum of your expression? Who had the largest expression? What is the largest expression that we can find? How are you using your knowledge of place value to get closer to 1000?

For the finale of this session, we explained our making thinking visible and building thinking classrooms pedagogy. Ultimately, our goal is thinking (not answer-getting), so… the work is not really ever finished. We launched Task 8: Carnival Conundrum from Mathematics Tasks for the Thinking Classroom, Grades K-5 by Peter Liljedahl and Maegan Girous. This task offers learners opportunities to build critical academic and character foundation skills. It also layers knowledge, concepts, and strategies to grow intellect and empathy, strengthens reasoning and retention, and cultivates new learning collectively and collaboratively.

Here’s what it looked like during our parent session.

We believe everyone can become a successful mathematician.  Thinking critically, problem-solving, and demonstrating number flexibility lead students to make connections to the real world.  We hope our parents felt the difference in the way we learn and teach numeracy. We definitely want them as our partners!