We have been back at school for 4 days. The first day was dedicated to exam analysis, exam corrections, and peer editing. The second day we talked briefly about graphing simple exponential function and negative exponents and then worked more on their exams. After school the usual crew worked in my room to complete their homework. I was really surprised to be asked “Ms. Gough, what level are these questions?” In an earlier blog post, Deep Practice, Leveling, and Communication, I wrote about the formative assessment with levels that is my team’s current assessment experiment. On day 3, we decided to go ahead with a formative assessment on computational fluency with negative exponents and then have students investigate exponential growth with an investigation using M&Ms. We were hesitant to give this assessment so early, but we thought it might serve as a diagnostic assessment too.
Let me stop here and offer our current thinking about the scoring and levels on this type of formative assessment. These assessments are not graded. They are taken individually as if taking a test. The assessments are self-scored, and then our learners complete a table of specifications to help us all determine their level of proficiency and where they need support. They are to work together to correct any problems up through level 3 and are encouraged to work on level 4 if they are moderately successful with level 3.
Level 1 – We try to target the most basic of the prerequisite skills necessary for this learning target.
Level 2 – We try to assess a prerequisite area that might cause our learners to stumble based on our history and experience with learners of this age.
Level 3 – This is the target level. Can our learners function at the desired level?
Level 4 – This is an enrichment level. If you are functioning on target, can we challenge you to learn more? These questions generally come from either the Honors Algebra I or the Algebra II learning targets.
If formative assessment informs the teachers and learner and causes a change in practice or behavior, then this was definitely formative assessment. The M&Ms were out on the table ready to be tossed and counted. As I looked through their tables of specifications, I learned that hardly anyone was working confidently at level 3. So, we took a poll. Do we postpone the M&M lab to work more on negative exponents? Rarely do I get 100% agreement, but today I did. “Yes, please Ms. Gough. We need to work more on negative exponents. And, will you teach us about exponents that are fractions?”
It was great! DD, my friend and teammate, was there to observe the M&M experiment. We agreed with our learners that the best decision was to stop and teach more about negative exponents; how often are we asked to teach something?
Here are three examples of my learners work and reflections from this formative assessment.
Isn’t it interesting that VB still puts a score on her paper, but MC and CL do not? We can quickly see that VB needs pay attention to a few details and needs to be challenged to move to level 4. MC needs to read the directions more carefully as well as correct her work and complete the table of specifications correctly. She understands whole number exponents, but needs a little coaching on how to write her answers. She may not understand the term evaluate, or she may need to read the directions. MC also needs help with fractions and arithmetic, but she understands negative exponents. CL is unclear when the exponent is zero and might need a refresher with fractions. She needs to pay attention to parentheses and should be encouraged to investigate fractional exponents.
One other thing to notice…CL reported 50% at level 3 and marked that this is the level where the work is most consistently correct. I just had to ask. Her response “yeah, if you look at my work, I messed up multiplying fractions and the zero exponent. I got negative exponents. You don’t have to worry about me.” I spend about the same amount of time with these formative assessments as I did when I gave quizzes, but now my job is more interesting. It is problem-solving, coaching, and having conversations with my learners. They have the opportunity to critique their work and report back to me. I feel like I’m coaching rather than judging. My learners talk to me about what they can do and what they need.
Does the formative assessment and table of specifications help these learners identify where they are and where we want them to be by the end of the unit? Will it help us know how to plan and teach? Does it tell us all where gaps are that need to be filled? Can we work together to close each gap?
Don’t you love CL’s reflection? “I think I need more help with Integers and exponents with rational numbers. With rational numbers, I feel like I had no idea what was going on, and like I hadn’t learned that stuff yet.”
It is about learning.
Experiments in Learning by Doing 
Jill,
First of all, I love these formative assessments. You’ve somehow managed be the perfect “mathematical trainer” for all of your students simultaneously, giving them a “workout” that scales to meet their level. The next step is just out for a student is just out of reach, yet they know it’s achievable with a bit of hard work. I’m going to have to think seriously this summer about trying to do something like this in physics. Also, have you seen the really cool way Kate Nowak was able to have kids self check group practice problems by implementing a checksum where kids totaled the answers to the practice problems and compared it to the answer Kate provided? In this way, no kid ever got to see the “answer” and so when their checksum didn’t add up, they had to do some soul searching among the for practice problems to figure out where the error was. This might be a fun thing to try every once in a while.
I have a larger question about exponents in general. Clearly, this exercise is all about mastering the various procedures for dealing with exponents, but I wonder if the students ever learn, or are assessed on what they mean. For example, what does
mean, and why would would you ever use it?
What gets me thinking of this is this very interesting post at Better Explained about why 0^0 =1, and how students need to expand their model of multiplication from repeated addition to scaling, and of exponents from repeated multiplication to growth. He presents a nice model of an “expand-o-tron” and sets up a model for thinking about exponents as
. So you could read 
as “start with 1, and triple it for 1.5 units of time, which is the product of tripling it 
and the square root of tripling it (
. And negative exponents could be viewed as shrinking.
Anyway, this is problem confused and rambly, but it gets me wondering if 8th graders are capable of reasoning about exponents in this way, so that they can have some sense of what they mean when they’re doing the calculation, and perhaps more importantly, a way to check if they’ve got the right answer when they calculate
= 
It seems to me one of the most important things I’d want kids to know when calculating something like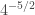 
are answers to questions like, should you answer be positive or negative? Why? Bigger or smaller than 4? why?
Secondly, I love the M&M experiment, but I wonder if might use this, or something like it (some other model of growth, like the classic rice/chessboard thing) to create a WCYDWT to get the kids to start thinking about how to use exponents, before they get too far into the weeds of the procedures. It might be fun to even do both, showing exponential growth, then decay to motivate positive/negative exponents.
Anyway, this post, as you can tell really got me thinking. Thanks so much!
LikeLike
[…] we jump into a new chapter, our class usually takes a formative assessment to tell us where we are and what we know before we actually start learning from Mrs. Gough. I take […]
LikeLike
[…] table of specifications helps our learners self-assess and calibrate their learning and understanding as we are working through the targets and […]
LikeLike
[…] Learning from Leveling, Self-Assessment, and Formative Assessment – “I spend about the same amount of time with these formative assessments as I did when I gave quizzes, but now my job is more interesting. It is problem-solving, coaching, and having conversations with my learners. They have the opportunity to critique their work and report back to me. I feel like I’m coaching rather than judging. My learners talk to me about what they can do and what they need.” […]
LikeLike
[…] Computational fluency: Negative Exponents (Algebra I) […]
LikeLike
[…] My artifact for today’s discussion along with my reflection answering the questions above can be seen in the post Learning from Leveling, Self-Assessment, and Formative Assessment. […]
LikeLike
[…] Example 1: Algebra I – I can evaluate an expression involving exponents that are integers. […]
LikeLike
[…] Learning from Leveling, Self-Assessment, and Formative Assessment This blog post has the negative exponents Algebra I example with student work. […]
LikeLike
[…] Learning from Leveling, Self-Assessment, and Formative Assessment This blog post from Jill has the negative exponents Algebra I example with student work. […]
LikeLike
[…] Learning from Leveling, Self-Assessment, and Formative Assessment This blog post from Jill has the negative exponents Algebra I example with student work. […]
LikeLike
[…] Learning from Leveling, Self-Assessment, and Formative Assessment […]
LikeLike